从某地区高中二年级学生中随机抽取质量监测数学得分在 120 分以下和 120 分以上(含 120 分) 的学生各 250 名作为样本(全体高二学生均参加监测), 分别测出他们的注意力集中水平得分, 统计如表.
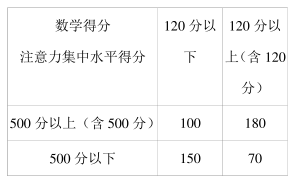
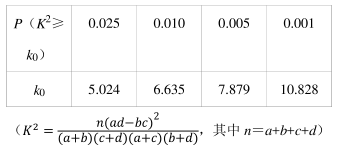
(1) 若将学生在质量监测中数学得分在 120 分以上(含 120 分). 定义为数学成绩优秀,将学生注意力集中水平得分在 500 分以上(含 500 分) 称为注意力集中水平高; 试问:能否有 99%以上的把握认为数学成绩优秀与注意力集中水平高有关?
(2) 若将上述样本的频率视为概率, 现从该地区所有高二学生中随机抽取 100 人, 设抽取到的数学得分在 120 分以上(含 120 分) 且注意力集中水平得分在 500 分以上(含 500分) 的人数为随机变量 X, 求 X的数学期望.



已知集合 A={x∈Z|﹣ 3<x<5}, B={y|y=2x, x∈A}, 则 A∩ B 的元素个数为()


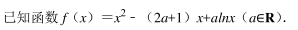



某地高中年级学生某次身体素质体能测试的原始成绩采用百分制, 已知这些学生的原始成绩均分布在[50, 100]内, 发布成绩使用等级制, 各等级划分标准见下表, 并规定: A, B, C 三级为合格, D 级为不合格

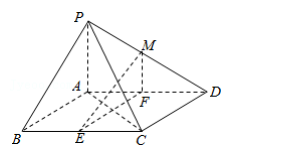
如图, 在四棱锥 P﹣ ABCD 中, 底面 ABCD 是平行四边形, ∠BCD=135° ,侧面 PAB⊥底面 ABCD, ∠BAP=90° , AB=AC=PA=2, E, F分别为 BC, AD 的中点,点 M在线段 PD 上.



为迎接 2022 年北京冬奥会, 桂林市某中学举办了“迎接冰雪之约, 奔向美好未来” 的奥运知识竞赛, 知识竞赛规则如下: 在预设的 6 个问题中, 选手若能连续正确回答出 3 个问题, 即停止答题, 晋级下一轮. 假定某选手正确回答每个问题的概率都是 2/3,且每个问题的回答结果相互独立, 则该选手至少回答了 5 个问题晋级下一轮的概率等于