当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概
“中心对称和中心对称图形”的教学目的主要有①知道中心对称的概念,能说出中心对称的定义和关于中心对称的两个图形的性质。②会根据关于中心对称图形的性质定理2的逆定理来判定两个图形关于一点对称;会画与已知图形关于一点成中心对称的图形。此外,通过复习图形轴对称,并与中心对称比较,渗透类比的思想方法;用运动的观点观察和认识图形,渗透旋转变换的思想。
通过题干来完成下列教学设计。
(1)给出本课程的课题引入;(14分)
(2)根据教学目标设计教学环节;给出两个实例以进行知识探究。(16分)
(1)课题引入:(引导性材料)
想一想:怎样的两个图形叫作关于某直线成轴对称?成轴对称的两个图形有什么特点?
(帮助学生复习轴对称的有关知识,为中心对称教学做准备)
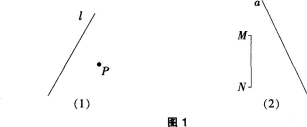
画一画:如图1(1),已知点P和直线ι,P出点P关于直线Z的对称点P′;如图1(2),已知线段MN和直线a,匦出线段MN关于直线a的对称线段M′N′。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答,教师作必要的提示,并归纳总结成下表:
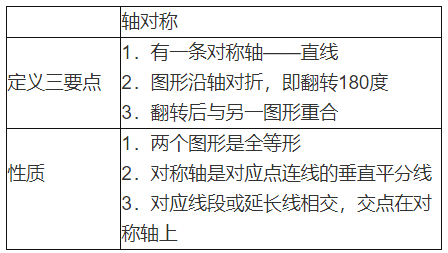
观察与思考:图2所示的图形关于某条直线成轴对称吗?如果是,画出对称轴;如果不是,说明理由。
(教师把图2的两个图形制成投影片或教具,学生仔细观察后,能发现这两个图形都不是轴对称。然后,教师适时提出问题:这两个图形能不能重合?怎样才能使这两个图形重合呢?让学生观察、探究、讨论,教师可以直观地演示中心对称变换的过程,让学生发现:把其中一个图形统一特殊点旋转180度后能与另一个图形重合。)
问题1:你能举出1~2个实例或实物.说明它们也具有上面所说的特性吗?
说明:学生自己举例有助于他们感性地认识中心对称的意义。然后,教师指出:具有这种特性的图形叫作中心对称图形.并介绍对称中心,对称点等概念。
问题2:你能给“中心对称”下一个定义吗?
说明与建议:学生下定义会有困难,教师应及时修正,并给出明确的定义,然后指出定义中的三个要点:
①有一个对称中心——点;②图形绕中心旋转180度;③旋转后与另一图形重合。把这三要点填入引导性材料中的空表内,在顶空格内写上“中心对称”字样,以利于写“轴对称”进行比较。
(2)教学环节:
环节1:练一练:在图3中,已知△ABC和△EFG关于点O成中心对称,分别找出图中的对称点和对称线段。
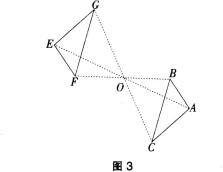
说明与建议:教师可演示△ABC绕点O旋转180度后与△EFG重合的过程,让学生说出点E和点A,点B和点F,点C和点G是对称点;线段AB和EF、线段AC和EG,线段BC和FG都是对称线段。教师还可向学生指出,上图中,点A、O、E在一条直线上,点C、O、G在一条直线上,点B、O、F在一条直线上,且AO=EO,BO=FO,CO=GO。
问题:从上面的练习及分析中,可以看出关于中心对称的两个图形具有哪些性质?
说明与建议:引导学生总结出关于中心对称的两个图形的性质:定理1——关于中心对称的两个图形是全等形;定理2——关于中心对称的两个图形,对称点连线都经过对称中心,并且被对称中心平分。
问题:定理2的题设和结论各是什么?试说出它的逆命题。
说明与建议:学生解答此题有困难,教师要及时引导。特别是叙述命题时。学生常常照搬“对称点”“对称中心”这些词语,教师应指出:由于没有“两个图形关于中心对称”的前提。所以不能使用“对称点”“对称中心”这样的词语,而要改为“对应如”“某一点”。最后,教师应完整地叙述这个逆命题——如果两个图形的对应点连线都经过某一点,并且被这一点平分。那么这两个图形关于点对称。
问题:怎样证明这个逆命题是正确的?
说明与建议:证明过程应在教师的引导下,师生共同完成。由已知条件——对应点的连线都经过某一点,并且被这一点平分,可以知道:若把其中一个图形绕着这点旋转180度,它必定与另一个图形重合,因此,根据定义可以判定这两个图形关于这一点对称。这个逆命题即为逆定理。根据这个逆定理,可以判定两个图形关于一点对称,也可以画出已知图形关于一点的对称图形。
环节2:练一练:画出图4中,线段PQ关于点O的对称线段P′Q′。
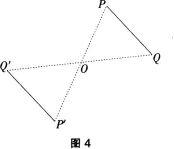
(画法如下:(1)连结PO,延长PO到P′,使OP′=OP,点P,就是点P关于点O的对称点。(2)连结QO,延长QO到Q′,使Q′Q=OQ,点Q′就是点Q的对称点,则PQ′就是线段PQ关于O点的对称线段。教师应指出:画一个
图形关于某点的中心对称图形,关键是画“对称点”。比如,画一个三角形关于某点的中心对称三角形,只要画出三角形三个顶点的对称点,就可以画出所要求的三角形。)
有“泥土诗人”之称的诗人是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
明朝初年强化君主专制的措施是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
《大碗岛的星期天》是哪一位画家作品?( )
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )
杜甫诗句“三月三日天气新,长安水边多丽人。”能够使人联想到的美术作品是()。
