当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->参数方程的教学要求是:把向量转化为坐标,获得了直线的参数方程
参数方程的教学要求是:把向量转化为坐标,获得了直线的参数方程,在此基础上分析直线参数方程的特点,体会参数的几何意义。
在此基础上完成下列教学任务:
(1)设计参数方程的三维教学目标;(9分)
(2)设计两种参数方程的引入方法;(15分)
(3)分析两种方法的优点。(6分)
(1)三维教学目标: 知识与技能:通过分析抛射物体运动中时间与物体位置的关系,了解一般曲线的参数方程, 体会参数的意义。
过程与方法:选取适当的参数,求简单曲线的参数方程。
情感、态度与价值观:通过观察、探索、发现的创造性过程,培养创新意识。
(2)复习导入法:回忆旧知,导入新课,教师提出问题:
①在平面直角坐标系中,确定一条直线的几何条件是什么?
②根据直线的几何条件,你认为应当怎样选择参数,如何建立直线的参数方程?
情景导入法:
引例1:一架救援飞机在离灾区地面500 m高处以100 m/s的速度作水平直线飞行.为使投放救援物资准确落于灾区指定的地面(不记空气阻力),飞行员应如何确定投放时机呢?救援物资做何运动?你能用物理知识解决这个问题吗?
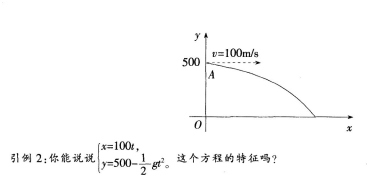
①有几个变量?
②x,y都可以用什么来表示?
③给定t的一个值,方程中x,y的值确定吗?
(3)情景引入法的优点:通过创设情景激发学生兴趣,提高学生学习的积极性,并且在创设情景的过程中有利于利用一个熟悉的参照物,帮助学习者将一个要探索的概念与熟悉的经验联系起来,并建立生活与数学之间的联系,引导他们利用这些经验来解释、说明,形成自己的知识。创设的情景好,吸引学生积极的参与和主动的学习,他们会体味到数学的美和趣味。
复习引入方法的优点:承上启下,使学生有准备、有目的地进入新课的学习,对于接下来的学习有很大的帮助,也为引导学生从几何条件思考参数的选择,为学生推导直线的参数方程做好准备。
有“泥土诗人”之称的诗人是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
明朝初年强化君主专制的措施是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
《大碗岛的星期天》是哪一位画家作品?( )
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )
杜甫诗句“三月三日天气新,长安水边多丽人。”能够使人联想到的美术作品是()。
