当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->“不等式”是高中数学必修5的内容。《普通高中数学课程标准》(
“不等式”是高中数学必修5的内容。《普通高中数学课程标准》(实验)要求学生能“通过具体情境,感受在现实世界和日常生活中存在着大量的不等关系,理解不等式(组)对于刻画不等关系的意义和价值;掌握求解一元二次不等式的基本方法,并能解决一些实际问题;能用二元一次不等式组表示平面区域,并尝试解决一些简单的二元线性规划问题;认识基本不等式及其简单应用;体会不等式、方程及函数之间的联系”。
(1)请设计一道利用不等式知识解决的实际问题并求解;(20分)
(要求:给出问题情境;抽象出数量关系;建立数学模型;写出解答过程、讨论和反思)
(2)根据上面的问题隋境设计一道开放题或探索题。(10分)
(1)问题情境:某地现有耕地10000公顷,规划10年后粮食单产比现有增加22%,人均粮食产量比现在提高10%,如果人口年增长率为1%,那么耕地每年至多只能减少多少公顷(精确到1公顷)?
分析:此题以关系国计民生的耕地、人口、粮食为背景,给出两组数据,要求考生从两条线索抽象数列模型,然后进行比较与决策。
读题:问题涉及耕地面积、粮食单产、人均粮食占有量、总人口数及三个百分率,其中人均粮食占有量P=粮食单产×耕地面积÷总人口数,主要关系是:P实际≥P规划。
建模:设耕地面积平均每年减少x公顷,现在粮食单产为a吨/公顷,现在人口数为m,则现在占有量为

评价:答案x≤4公顷符合控制耕地减少的国情,又验算无误,故可作答。
讨论与反思:本题主要是抓住各量之间的关系,注重3个百分率。其中耕地面积为等差数列,总人口数为等比数列模型,问题用不等式模型求解。本题的解法是建立不等式模型,要求对指数函数、不等式、增长率、二项式定理应用于近似计算等知识熟练。此种解法可以解决有关统筹安排、最佳决策、最优化等问题。此种题型属于不等式模型,也可以把它作为数列模型,相比之下,主要求解过程是建立不等式模型后解出不等式。在解答应用问题时,我们强调“评价”这一步不可少!它是解题者的自我调节,比如本题求解过程中若令1.0110≈1,算得结果为x≤98公顷,自然会问:耕地减少这么多,符合国家保持耕地的政策吗?于是进行调控,检查发现是错在1.0110的近似计算上。
(2)甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x),g(x)以及任意的x≥0,当甲公司投入x万元做宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元做宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
①试解释f(0)=10,g(0)=20的实际意义;
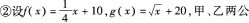
司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
有“泥土诗人”之称的诗人是()。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
明朝初年强化君主专制的措施是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
下列国家中,建造了胡夫金字塔的是()。