当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->“几何概型”是高中阶段学生的必修内容,被安排在“古典概型”内
“几何概型”是高中阶段学生的必修内容,被安排在“古典概型”内容之后学习。在现实生活中,常常会遇到试验的所有可能结果是无穷多的情况,这时就不能用“古典概型”来解决了。在特定情形下,可以用“几何概型”来解决此类问题。
请完成下列任务:
(1)请设计高中“几何概型”这一内容的教学目标;
(2)请结合教学目标,类比“古典概型”设计“几何概型”的主要教学过程;
(3)设计下述习题的变式题(写出答案),并总结出求解几何概型问题的步骤。
习题:在等腰直角三角形ABC中,∠B=90°,在线段AC上任取一点P,求AP<AB的概率。

①问题1古典概型中的6个基本事件为“取得值为0”“取得值为1”“取得值为2”“取得值为3”“取得值为4”“取得值为5”,“取得值不小于3”包含3个基本事件,为“取得值为3”“取得值为4”“取得值为5”,故P(取得值不小于3)=
②问题2为几何概型,区域D的长度为5,区域d的长度为2,故P(取得值不小于3)=
5.拓展延伸:上述边长为8 cm的正方形及其内切圆,随机向正方形内丢一粒黄豆,求黄豆落入圆心的概率。
学生讨论,教师总结:概率为0。如果随机事件所在区域是一个单点,则它出现的概率为0,但它不是不可能事件;如果随机事件所在区域是全部区域扣除一个单点,则它出现的概率为1,但它不是必然事件。
(3)习题变式题:在等腰直角三角形ABC中,∠B=90°,在∠ABC内作射线BP交线段AC于点P,求使得AP<AB的概率。

解题过程:在线段AC上取一点M使得AB=AM,如图所示。

包含所有基本事件的区域D为∠ABC=90°。
假设“AP<AB”为事件A,事件A所对应的区域d为∠ABM=67.5°。


解几何概型问题的步骤:
①判断该概率模型是不是几何概型;
②如果是,注意几何度量的选择;
③把实际问题中的度量关系转化成长度、面积、体积等形式;
④根据几何概型计算公式求出概率。
(1)教学目标
①知识与技能目标:正确理解几何概型的概念,掌握几何概型的概率计算公式,会根据古典概型和几何概型的区别与联系来判别某种概型是古典概型还是几何概型。
②过程与方法目标:在探究学习的过程中,体会数学知识的形成,数学知识与现实世界的联系;学会应用数学知识来解决实际问题,提高逻辑推理能力;
③情感态度与价值观目标:在学习的过程中,培养严谨的学风,感受数学来源于生活,应用于生活。
(2)教学过程
一、旧知回顾
带领学生回顾古典概型的旧知内容。
二、引入新知
问题1:若x的取值是区间[0,5]中的整数,任取一个x的值,求“取得值不小于3”的概率。(古典概型)
问题2:若x的取值是区间[0,5]中的实数,任取一个x的值,求“取得值不小于3”的概率。(几何概型)学生自主讨论、比较问题1,2的不同,引入新知——“几何概型”。
三、新知探究
1.试验:取一个边长为8 cm的正方形及其内切圆,随机向其中丢一粒黄豆,那么黄豆落入圆内的概率有多大?
学生利用模具自主探究,教师指导,最终形成下表。


2.几何概型的概念:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型。在几何概型中,事件A的概率的计算公式如下:
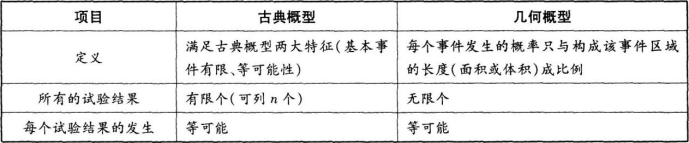
3.活动:让学生对比古典概型,找出古典概型和几何概型之间的区别和联系。
学生讨论、教师指导后形成下表。
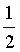
引入部分问题探究:让学生自主探究课堂开始的两个问题,形成答案后汇报,教师点评、指导,订正答案:
①问题1古典概型中的6个基本事件为“取得值为0”“取得值为1”“取得值为2”“取得值为3”“取得值为4”“取得值为5”,“取得值不小于3”包含3个基本事件,为“取得值为3”“取得值为4”“取得值为5”,故P(取得值不小于3)=②问题2为几何概型,区域D的长度为5,区域d的长度为2,故P(取得值不小于3)=
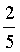
5.拓展延伸:上述边长为8 cm的正方形及其内切圆,随机向正方形内丢一粒黄豆,求黄豆落入圆心的概率。
学生讨论,教师总结:概率为0。如果随机事件所在区域是一个单点,则它出现的概率为0,但它不是不可能事件;如果随机事件所在区域是全部区域扣除一个单点,则它出现的概率为1,但它不是必然事件。
(3)习题变式题:在等腰直角三角形ABC中,∠B=90°,在∠ABC内作射线BP交线段AC于点P,求使得AP<AB的概率。
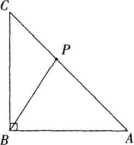
解题过程:在线段AC上取一点M使得AB=AM,如图所示。
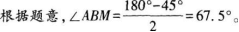
包含所有基本事件的区域D为∠ABC=90°。
假设“AP<AB”为事件A,事件A所对应的区域d为∠ABM=67.5°。
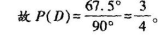
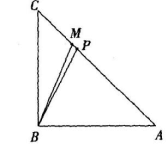
解几何概型问题的步骤:
①判断该概率模型是不是几何概型;
②如果是,注意几何度量的选择;
③把实际问题中的度量关系转化成长度、面积、体积等形式;
④根据几何概型计算公式求出概率。
有“泥土诗人”之称的诗人是()。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
明朝初年强化君主专制的措施是()。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
下列国家中,建造了胡夫金字塔的是()。
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
马老师在活动反思中写道:"使用档案袋对幼儿的表现进行评价,经常需要花费些额外的时间,与其在这些花样上花时间,不如把精力多用在孩子身上。”这边明马老师()