当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->针对“函数的奇偶性”的教学,教师制定了以下教学目标:①理解函
针对“函数的奇偶性”的教学,教师制定了以下教学目标:
①理解函数的奇偶性的概念,进一步掌握判断函数奇偶性的方法;
②感悟数形结合的思想,体会奇偶函数图像的特征和意义。
基于上述内容,完成下列任务:
(1)基于教学目标①,设计一个实例,总结判断函数奇偶性的步骤;
(2)写出“函数的奇偶性”的教学重点和难点;
(3)设计一个教学引入片段,并说明设计意图。
(1)实例:判断函数
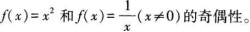
判断函数奇偶性的步骤:①判断定义域是否关于原点对称,若定义域不关于原点对称,则此函数为非奇非偶函数;②判断f(-x)=f(x)或f(-x)=-f(x)是否成立;③若f(-x)=f(x)成立,此函数为偶函数;若f(-x)=-f(x)成立,此函数为奇函数。
(2)重点:函数奇偶性的概念及其判断方法。
难点:对函数奇偶性概念的理解及如何判断函数奇偶性。
(3)教学引入片段
教师首先进行课堂提问,随机挑选学生回答。
提问1:谁能说说函数的定义是什么?
提问2:什么是函数的定义域?值域呢?
【设计意图】在新课开始前让学生回顾上节课的知识,一方面帮助学生巩固已学的旧知识,另一方面为新课的引入做好铺垫。
教师课件上出示4个函数,让学生独立在纸上大致画一下四个函数的图像。教师随机挑选学生回答这四个函数的图像特征(在学生回答问题时,教师应适时引导学生往函数图像的对称性上思考)。
(1)y=x2
(2)y=(x-1)2
(3)y=x3
(4)y=x+1
教师总结结论:函数(1)的图像关于Y轴对称;函数(2)的图像关于x=1对称;函数(3)的图像关于原点对称;函数(4)的图像关于x,y轴以及原点都没有对称性。
在总结结论后,教师表述函数图像对称性类似(1)和(3)的函数是特别的,顺势引入函数奇偶性的教学。
【设计意图】以具体的函数实例入手,让学生动手画图并根据所画函数图像探索不同函数的函数图像具有不同的特征,从而顺势引入新课。这有助于培养学生的实际动手能力,从而掌握研究函数的基本方法——画图,还有助于培养学生探索、分析问题并得出结论的数学素养。
有“泥土诗人”之称的诗人是()。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
明朝初年强化君主专制的措施是()。
将下列各项按所表示年龄大小顺序排列,正确的顺序应是( )。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
钱穆在评论中国古代某制度时说,它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”,这一制度是()。
1931年,一位给人们带来光明的科学家重病的消息牵动着世界人民的心,几十名记者为他守夜。每隔一个小时就对外发布一次消息:“灯”还亮着。这位科学家是( )。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
下列国家中,建造了胡夫金字塔的是()。