当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->在“一元二次方程根与系数的关系”一课上,某教师设计如下的教学
在“一元二次方程根与系数的关系”一课上,某教师设计如下的教学过程:
一、探究规律
先填空,再找规律: 
思考:观察表中x1+x2与XlX2的值,它们与前面的一元二次方程的各项系数之间有什么关系 从中你能发现什么规律
二、得出定理并证明(韦达定理)若一元二次方程
的两根为xl、x2,则
特殊的:若一元二次方程x2+px+q=0的两根为x1、x2,则
x1+x2=-pxlx2=q
证明此处略(师生合作完成)
阅读上述教学设计片段,完成下列任务:
(1)请为此教学片段设计一个导入过程,并写出设计意图。(10分)
(2)分析该教师设计这两个环节的意图。(8分)
(3)请为此教学片段设计课堂练习并写出理由。(12分)
(1)导入过程:
我们知道生活中许多事物存在着一定的规律,有人发现并验证后就得到伟大的定理.比如:
抛出的重物总会落下(万有引力定律——牛顿)
电路中的电流、电压、电阻存在一定关系:U=IR(欧姆定律——欧姆)
而我们数学学科中更蕴藏着大量的规律,比如:
直角三角形的三边a,b,C满足关系:a2+b2=c2(勾股定理——毕达哥拉斯)
那么一元二次方程中是否也存在什么规律呢 今天共同去探究,感受一次当科学家的味道。
设计意图:让学生感受到数学和其他学科一样,里边有很多有价值的规律,等待我们去探索,激发学生的学习兴趣,探究欲望。
(2)探究规律环节的设计意图:通过学生计算一些特殊的一元二次方程的两根之和与两根之积,启发学生从中发现存在的一般规律,渗透特殊到一般的思想方法。
得出定理并证明环节的设计意图:让学生自己发现规律,找到成功感,再从理论上加以验证,让学生经历从特殊到一般的科学探究过程。
(3)例1.求下列方程的两根之和与两根之积。


设计意图:进一步巩固根与系数的关系,体会“整体代人”思想在解题中的运用,可起到简便运算的作用。
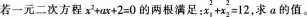
设计意图:它是例2的一个变式,目的是考察学生灵活运用知识解决问题的能力,让学生感受到根与系数的关系在解题中的运用,同时也考察学生思维的严密性,根据情况可再进一步变式,如两根互为相反数;两根的倒数和等于2等。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
教师职业道德区别于其他职业道德的显著标志就是( )。
对高中数学的评价,下列说法错误的是( )。
