当前位置:首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->教学内容:人教版七年级数学上册第96页中的片段:下面的框图表
教学内容:人教版七年级数学上册第96页中的片段:
下面的框图表示了解这个方程的流程:

根据上述提供的教学内容,完成下列任务:
(1)提炼出“解一元一次方程”的一般步骤;
(2)预设学生在学习“解一元一次方程”过程中可能出现的错误,并提出你的矫正策略;
(3)类比法是数学教学中一种重要的教学方法,请你结合学生学习“解一元一次方程”的经验,设计一个“解一元一次不等式”的教学片段。
(1)“解一元一次方程”的一般步骤如下: ①去分母:方程两边都乘以各分母的最小公倍数;
②去括号:根据去括号法则和乘法分配律依次去各级括号;
③移项:将含有未知数的项移到方程的一边,其他项移到另一边;
④合并同类项:将方程化为ax=b(a≠0)的形式;

(2)可能出现的错误,原因及解决方法
预设1:去括号时,不能正确运用乘法分配律
例1.解方程3(x+2)=2(x-8)
错解:3x+2=2x-16
正确解法:3x+6=2x-16
错误地方:在应用乘法分配律去3(x+2)中的括号时,3没有和2相乘。
错误原因:不会正确应用乘法分配律,对乘法分配律理解不透,即分配不均。
解决办法:复习巩固乘法分配律。
预设2:去括号时,括号前面的负因数中负号没有兼顾
例2.解方程2x=8-2(x+3)
错解:2x=8-2x+6
正确解法:2x=8-2x-6
错误地方:在去括号时,把括号前面的“-”看成运算符号,把2与括号里进行分配,这里的括号应该还没去掉,少了再去括号这一步。
错误原因:运算符号和性质符号混淆不清。若把2前面的“-”看成减号。应该先把2用乘法分配律进行分配,再按去括号法则去括号;若把“-“看成性质符号,在进行乘法分配律时就把-2与括号里每一项相乘。
解决办法:①把2前面的“-”号看成性质符号,把-2x进行分配;
②分两步,即先把2按照乘法分配律进行分配,再根据去括号法则去括号。
预设3:去分母时,不含分母的项漏乘
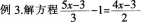
错解:2(5x-2)-1=3(4x-3)
正确解法:2(5x-2)-6=3(4x-3)
错误地方:在应用等式的性质时-1没有和6相乘.就是常说的漏乘。
错误原因:对等式的性质没有熟练掌握,不能灵活运用。
解决办法:复习巩固等式的性质以及乘法分配律的灵活运用。
预设4:去分母时,分子是多项式没有打括号
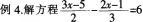
错解:方程两边都乘6得:9x-15-4x-2=36
正确解:方程两边都乘6得:3(3x-5)-2(2x-1)=36
错误地方:去分母后分子是多项式没有打括号。
错误原因:不理解分数线在这里还具有括号的作用,去掉分母后,多项式分子要加括号。
解决办法:正确理解分数线的几种作用。
预设5:在化系数为1时,被除数和除数位置颠倒
例5.解方程2(3x-2)=2。
错解:去括号得:6x-4=-2
移项得:6x=-2+4
合并同类项得:6x=2
化系数为1得:x=3

错误原因:学生发现6正好能被2整除,误认为6就是被除数;对“在方程两边都除以6”这句话没有理解。
解决办法:①在化系数为1时,可以让学生在方程两边都乘未知数系数的倒数。②理解被除数和除数的意义和语言表达方式。
(3)“解一元一次不等式”的教学片段设计
(一)创设问题情境,引入新课
师:同学们,我们学过一篇课文《锯是怎样发明的》,你们知道为什么鲁班会发明锯吗他受到了怎样的启发
师:这种方法就是数学中常说的“类比思想”,今天这节课我想和大家一起去感受类比思想带给我们的启发。
(二)温故而知新
1.什么叫一元一次方程解一元一次方程的基本步骤是什么
只含有一个未知数,未知数的指数是一次,这样的方程叫作一元一次方程。
基本步骤是:a.去分母;b.去括号;c.移项;d.合并同类项;e.系数化为1。
观察下列不等式:
(1)2x-2.5≥15,(2)x≤8.75,
(3)x>4,(4)5+3x>240,
这些不等式有什么共同特征
(只含有一个未知数,未知数的最高次数是一次,都是整式)
师:大家给它们取个什么名字呢
2.一元一次不等式的定义
归纳:只含有一个未知数,未知数的最高次数是一次,这样的不等式叫一元一次不等式。
师:下面我们来判断下列不等式是不是一元一次不等式。请大家讨论。
小黑板出示:
下列不等式是一元一次不等式吗
(1)2x-2.5≥15,(2)5+3x>240,(3)x<-4,
(5)x2>0。
(1)(2)(3)中的不等式是一元一次不等式,(4)(5)不是。
师:好,从上面的讨论中,我们可以得出判断一元一次不等式的条件有三个,即未知数的个数,未知数的次数,且不等式的两边都是整式。请大家理解一元一次不等式的定义。
3.类比探索一元一次不等式的解法.
(1)比一比口答
①x的2倍等于6,求x;②x的2倍小于6,求x。
(2)练习板演
①x的2倍加1等于x的5倍加l0,求x;②x的2倍加1不小于x的5倍加10,求x。
(3)试一试指名板演
①解方程:3-x=2x+6②解不等式3-x<2x+6
学生讨论:解一元一次不等式和解一元一次方程的方法、步骤。
4.再探解一元一次不等式的一般步骤:
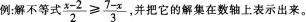
解:去分母,得3(x-2)≥2(7-x)
去括号,得3x-6≥14-2x
移项,合并同类项,得5x≥20
两边都除以5,得x≥4
这个不等式的解集在数轴上表示如下:

5.解一元一次不等式与解一元一次方程的区别与联系。
利用解一元一次方程与解一元一次不等式的方法、步骤都类似的结论,一起完成下面的表格(小黑板出示):
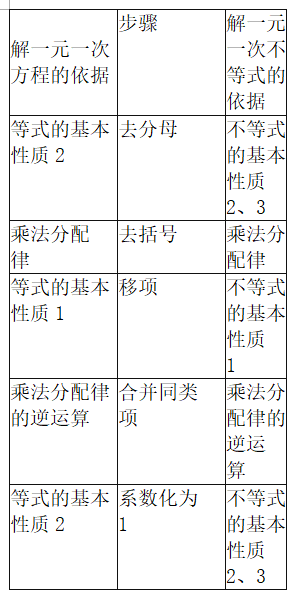
看来大家已经对解一元一次不等式的步骤掌握得很好了,请大家判断以下解法是否正确。若不正确,请改正。(小黑板出示)
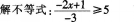
解:去分母.得-2x+1≥-15
移项、合并同类项,得-2x≥-16
两边同时除以-2,的x≥8
学生回答,教师重点强调:
区别:(1)不等式两边都乘以(或除以)同一个负数时,不等号的方向改变;而方程两边乘以(或除以)同一个负数时,等号不变。
(2)一元一次不等式有无限多个解,而一元一次方程只有一个解。
(三)课堂练习
解下列不等式。并把它们的解集分别表示在数轴上:
(1)5x>-10,(2)-3x+12≤0,
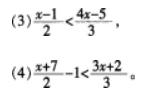
指名板演,学生评价,教师点评。
(四)课时小结
本节课学习了如下内容:
(1)一元一次不等式的定义
(2)一元一次不等式的解法
(3)解一元一次不等式与解一元一次方程的区别与联系(运用类比思想)
(五)课后作业(略)
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
教师职业道德区别于其他职业道德的显著标志就是( )。
对高中数学的评价,下列说法错误的是( )。
