当前位置:首页 → 职业资格 → 教师资格 → 中学生物学科知识与教学能力->为了调查某河流的水质状况,某研究小组测定了该河流水样中的细菌
为了调查某河流的水质状况,某研究小组测定了该河流水样中的细菌含量,并进行了细菌分离等工作。回答下列问题:
(1)该小组采用稀释涂布平板法检测水样中的细菌含量。在涂布接种前,随机取若干灭菌后的空白平板先行培养了一段时间,这样做的目的是_________;然后,将1 ml水样稀释100倍,在3个平板上用涂布法分别接入0.1 ml稀释液;经适当培养后,3个平板上的菌落数分别为39、38和37,据此可得出每升水样中的活菌数为_________。(6分)
(2)该小组采用平板划线法分离水样中的细菌,操作时,接种环通过_________灭菌,在第二次及以后的划线时,总是从上一次划线的末端开始划线,这样做的目的是_________。(6分)
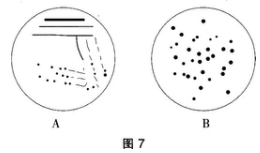
(3)图7中,_________表示的是用稀释涂布平板法接种培养后得到的结果。(3分)
(1)检测培养基平板是否灭菌合格:3.8×107(2)灼烧;将聚集的菌体逐步稀释以便获得单个菌落
(3)B
解析:(1)为了确定培养基的灭菌是否合格,微生物学实验一般会设置空白对照:随机取若干灭菌后的空平板培养一段时间,观察培养基上是否有菌落生成;利用平板菌落计数法的计算公式估算水样中的活菌数:
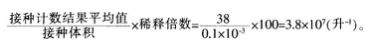
(2)接种时接种环需要灼烧灭菌;在第二次及以后划线时,总是从上一次的末端开始划线,这样做的目的是:通过划线次数的增加,使每次划线时菌体的数目逐渐减少,以便得到单个菌落。
(3)由题图可知A图为平板划线接种法,B图为稀释涂布平板法接种的结果(菌落分布相对均匀)。
《义务教育数学课程标准(2011年版)》强调,课程内容要反映社会的需要、数学的特点,要符合学生的认知规律。课程内容的组织要重视过程,处理好()的关系。
设α是某一方程组的解向量,k为某一常数,则kα也为该方程组的解向量。( )

案例:
在有理数运算的课堂教学片段中,某学生的板演如下:

针对该学生的解答,教师进行了如下教学:
师:请仔细检查你的演算过程,看是否正确无误?
生:好像正确吧。

请分析例题1、例题2中每一步运算的依据。(10分)
初中数学课程是一门国家课程,其主要内容包括课程目标、教学内容、教学过程和( )等
教师职业道德区别于其他职业道德的显著标志就是( )。
对高中数学的评价,下列说法错误的是( )。
