义务教育课程标准实验教科书《数学》人教版六年级下95页介绍了著名的“哥尼斯堡七桥问题”,请阅读教材,并回答下列问题。
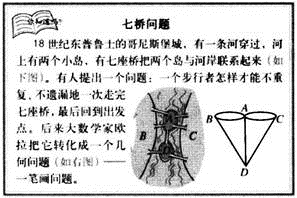
(1)步行者能否不重复不遗漏地一次走完七座桥呢?
(2)解决这个问题时,用到了“数学建模”思想,请结合七桥问题,阐述运用“数学建模”
思想解决实际问题的步骤。
(1)不能。
(2)建立数学模型的步骤:
①把实际问题加以提炼,抽象为数学问题。
在此例中,数学家欧拉把被河流隔开的小岛和三块陆地看成四个点,把每座桥看成一条线。这样“七桥问题”就抽象为四个点和七条线组成的几何图形,“七桥问题”就抽象概括为能否一笔且无重复的画出教材中抽象图形的问题。
②求出模型的解。
因为可以一笔且无重复地画出某一图形的充分必要是:图中各中间点的曲线段总是偶数条。然而,现在得出的图形中的四个交点A、B、C、D处所通过的曲线段都是奇数条,这不符合“一笔画”所具有的特征。因此,“七桥问题”无解。
③验证模型的合理性。学生可以通过观察实验验证无解。
④用模型提供的解答来解释现实问题。
“有为才有位,有位更有为”,这一看法给我们的启示是( )
对立统一规律揭示了事物发展的( )。
历史唯物主义认为人的价值在于( )
在认识过程中具有更为重要意义的飞跃是指()
矛盾的普遍性与特殊性的关系是( )
毛泽东第一次提出“马克思列宁主义理论和中国革命的实践相结合”这个根本思想原则的著作是( )
真理的具体性体现在( )。
“没有抽象的真理,真理总是具体的。”这一思想可以理解为( )。
“三个代表”重要思想是马克思主义中国化的最新理论成果。它与马克思列宁主义、毛泽东思想、邓小平理论是一脉相承的统一的科学理论。这种一脉相承具体表现在( )
在下列说法中,有助于提升从业人员职业道德的观点是( )
①“运筹帷幄之中,决胜千里之外”
②“勿以善小而不为,勿以恶小而为之”
③“舟必漏而后入水,土必湿而后生苔”