当前位置：首页 → 职业资格 → 教师资格 → 中学数学学科知识与教学能力->案例：下面是“零指数幂”教学片段的描述，阅读并回答问题。片段
案例：下面是“零指数幂”教学片段的描述，阅读并回答问题。
片段一：观察下列式子，指数有什么变化规律 相应的幂有什么变化规律 猜测20-
24=16
23=8
22=4
21=2
20=
上面算式中，从上向下每一项指数减1，幂减半，猜测20=1。
片段二：用细胞分裂作为情境，验证上面的猜测：一个细胞分裂一次变为2个，分裂2次变为4个，分裂3次变为8个……那么，一个细胞没有分裂时呢
片段三：应用同底数幂的运算性质：2m÷2n=2m-n(m，n为正整数，m>n)，我们可以尝试m=n的情况，有23÷23=23-3=20。根据23÷23=8÷8=1，得出：20-1。
片段四：在学生感受“20-1”的合理性的基础上，做出零指数幂的“规定”，即a0=1(a≠0)。验证这个规定与原有“幂的运算性质”是无矛盾的，即原有的幂的运算性质可以扩展到零指数幂。
问题：
(1)请确定这四个片段的整体教学目标；(6分)
(2)验证运算法则
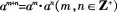可以拓展到自然数集；(5分)
(3)这四个片段对数学运算法则的教学有哪些启示 (9分)
(1)知识与技能目标：掌握整数指数幂的运算性质，理解零指数幂的意义，掌握数学中归纳总结的能力。
过程与方法目标：通过探索，让学生体会从特殊到一般的数学研究方法。
情感态度与价值观目标：培养学生的观察分析和根据规律探究问题的能力，加深对类比、找规律、严密的推理等数学方法的认识。培养学生的数学思维能力。
(2)当m．n中有一个为零时
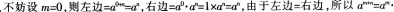
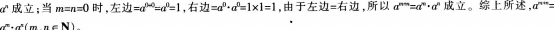
(3)从特殊到一般是研究数学的一个重要方法；可以在已有知识的基础上推导运算法则；观察分析和根据规律是数学运算法则教学中的一种方法；要注意学科之间的交叉性，可以用学生比较熟悉的其他学科的知识进行教学。
有“泥土诗人”之称的诗人是（）。
将下列各项按所表示年龄大小顺序排列，正确的顺序应是（ ）。
①不惑②垂髫③花甲④加冠⑤而立⑥古稀⑦半百
明朝初年强化君主专制的措施是（）。
钱穆在评论中国古代某制度时说，它“可以培植全国人民对政治之兴味……可以团结全国各地域于一个中央之统治”，这一制度是()。
1931年，一位给人们带来光明的科学家重病的消息牵动着世界人民的心，几十名记者为他守夜。每隔一个小时就对外发布一次消息：“灯”还亮着。这位科学家是（ ）。
《义务教育数学课程标准（2011年版）》强调，课程内容要反映社会的需要、数学的特点，要符合学生的认知规律。课程内容的组织要重视过程，处理好（）的关系。
《大碗岛的星期天》是哪一位画家作品？（ ）
设α是某一方程组的解向量，k为某一常数，则kα也为该方程组的解向量。（ ）
杜甫诗句“三月三日天气新，长安水边多丽人。”能够使人联想到的美术作品是()。
