“对任意给定的ε∈(0，1)，总存在正整数N，当n>N时，恒有｜xn-a｜≤2ε”是数列{xn}收敛于a的
本题主要考查考生对数列极限的ε-N定义的理解.其定义是“对任意给定的ε>0，总存在正整数N，当n>N时，恒有｜xn-a｜<ε”显然，若｜xn-a｜<ε，则必有｜xn-a｜≤2ε，但反之也成立，这是由于ε的任意性，对于任意给定的ε1>0，取｜xn-a｜≤2ε中的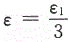
，则有
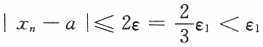即，对任意给定的正数ε1>0，总存在正整数N，当n>N时，恒有｜xn-a｜<ε1，故应选(C). 【评注】到目前为止，考研试卷中还没考过利用极限定义证明
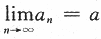，或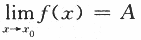
的试题，但从本题可看出，要求考生理解极限的定义.
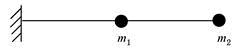
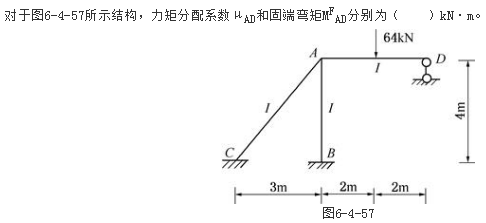
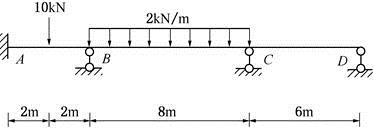
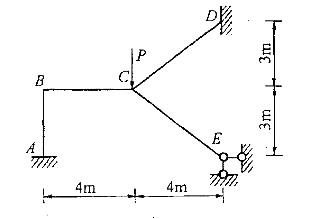
图示结构，各杆EI=常数，不计轴向变形，MBA及MCD的状况为:
