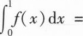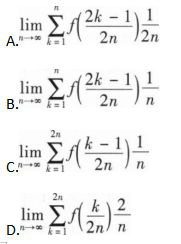设三阶矩阵A=(α1，α2，α3)，B=(β1，β2，β3)，若向量组α1，α2，α3可以由向量组β1，β2，β3线性表出，则（ ）．
因为向量组α1，α2，α3。可由向量组β1，β2，β3线性表出，所以存在矩阵C，使得A=BC，取转置得CTBT=AT，对于?α，BTα=0，则CTBTα=0，即ATα=0，故BTx=0的解均为ATX=0的解．
设平面区域D由曲线(x2+y2)2=x2-y2(x≥0，y≥0)与x轴围成，计算二重积分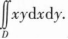
设y=y(x)(x>0)是微分方程xy'—6y=-6满足条件y(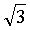
)=10的解．
(I)求y(x)；
(Ⅱ)设P为曲线y=y(x)上一点，记曲线y=y(x)在点P的法线在Y轴上的截距为Ip
当Ip最小时，求点P的坐标．
设函数f(x)满足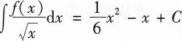
，L为曲线y=f(x)(4≤x≤9)，记L的长度为S，L绕x轴旋转所成旋转曲面的面积为A，求S和A
已知函数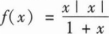
，求曲线y=f(x)的凹凸区间及渐近线．
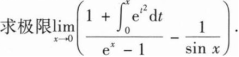
设三阶矩阵A=(α1，α2，α3)，B=(β1，β2，β3)，若向量组α1，α2，α3可以由向量组β1，β2，β3线性表出，则（ ）．
设函数f(x)=sec x在x=0处的2次泰勒多项式为1+ax+bx2，则（ ）．
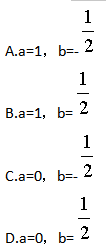
有一圆柱体，底面半径与高随时间变化的速率分别为2cm／s，-3cm／s，当底面半径为10cm，高为5cm时，圆柱的体积与表面积随时间变化的速率分别为（ ）．
设函数f(x)在区间[0，1]上连续，则
