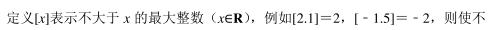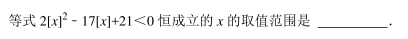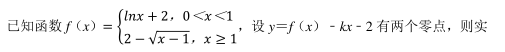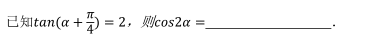赤道平面内的某颗卫星自西向东绕地球做圆周运动该卫星离地面的高度小于地球同步卫星的高度， 赤道上一观测者发现， 该卫星连续两次出现在观测者正上方的最小时间间隔为 t， 已知地球自转周期为 T 0 ， 地球半径为 R， 地球表面的重力加速度为 g， 由此可知该卫星绕地球运动的周期 T 和离地面的高度 H 为（）
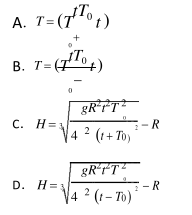
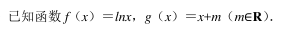
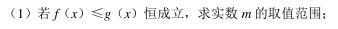
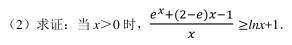
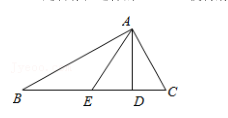
如图， 在△ABC 中， AB＞AC， AD、 AE 分别为 BC 边上的高和中线， AD＝4，DE＝3．
（1） 若∠BAC＝90° ， 求 AB 的长；
（2） 是否存在这样的△ABC， 使得射线 AE 和 AD 三等分∠BAC？
设函数 f（x） ＝﹣ x 2 +ax+b， 若不等式 f（x） ＞0 的解集为（﹣ 1， 3）．
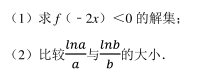
已知直线 y＝m 与函数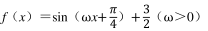
的图象相交， 若自左至右的三个相邻交点 A， B， C 满足 2|AB|＝|BC|， 则实数 m＝
